This is part 2/8 of my Calculating Percentiles on Streaming Data series.
The most famous algorithm for calculating percentiles on streaming data appears to be Greenwald-Khanna [GK01]. I spent a few days implementing the Greenwald-Khanna algorithm from the paper and I discovered a few things I wanted to share.
Insert Operation
The insert operation is defined in [GK01] as follows:
- INSERT(v)
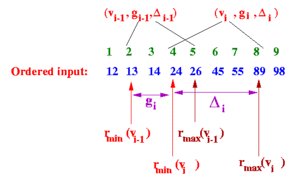
- Find the smallest i, such that vi−1≤v<vi, and insert the tuple tx=(vx,gx,Δx)=(v,1,⌊2ϵn⌋), between ti−1 and ti. Increment s. As a special case, if v is the new minimum or the maximum observation seen, then insert (v,1,0).
However, when I implemented this operation, I noticed via testing that there were certain queries I could not fulfill. For example, consider applying Greenwald-Khanna with ϵ=0.1 to the sequence of values 11,20,18,5,12,6,3,2, and then apply QUANTILE(ϕ=0.5). This means that r=⌈ϕn⌉=⌈0.5×8⌉=4 and ϵn=0.1×8=0.8. There is no i that satisfies both r–rmin(vi)≤ϵn and rmax(vi)–r≤ϵn, as you can see below:
| i | ti | rmin | rmax | r–rmin | rmax−r | r–rmin?≤ϵn | rmax–r?≤ϵn |
|---|---|---|---|---|---|---|---|
| (2,1,0) | 1 | 1 | 3 | -3 | F | T | |
| 1 | (3,1,0) | 2 | 2 | 2 | -2 | F | T |
| 2 | (5,1,0) | 3 | 3 | 1 | -1 | F | T |
| 3 | (6,1,1) | 4 | 5 | 0 | 1 | T | F |
| 4 | (11,1,0) | 5 | 5 | -1 | 1 | T | F |
| 5 | (12,1,0) | 6 | 6 | -2 | 2 | T | F |
| 6 | (18,1,0) | 7 | 7 | -3 | 3 | T | F |
| 7 | (20,1,0) | 8 | 8 | -4 | 4 | T | F |
I believe the fundamental problem is that the definition of INSERT(v) fails to maintain the key invariant maxi(gi+Δi)≤2ϵn. To correct this issue, the Greenwald-Khanna INSERT(v) operation must be modified as follows:
- INSERT(v)*
- Find the smallest i, such that vi−1≤v<vi, and insert the tuple tx=(vx,gx,Δx)=(v,1,⌊2ϵn⌋–1), between ti−1 and ti. Increment s. As a special case, if v is the new minimum or the maximum observation seen, then insert (v,1,0). Also, the first 1/(2ϵ) elements must be inserted with Δi=0.
I found the above modification from Prof. Chandra Chekuri’s lecture notes for his class CS 598CSC: Algorithms for Big Data. I believe this modification will maintain the above invariant after 1/(2ϵ) insertions.
Band Construction
Banding in [GK01] refers to the grouping together of possible values of Δ for purposes of merging in the COMPRESS operation. The paper defines banding as the following:
- BAND(Δ, 2ϵn)
- For α from 1 to ⌈log2ϵn⌉, we let p=⌊2ϵn⌋ and we define bandα to be the set of all Δ such that p–2α–(pmod2α)<Δ≤p–2α–1–(pmod2α–1). We define band0 to simply be p. As a special case, we consider the first 1/2ϵ observations, with Δ = 0, to be in a band of their own. We will denote by band(ti,n) the band of Δi at time n, and by bandα(n) all tuples (or equivalently, the Δ values associated with these tuples) that have a band value of α.
Here are some things I found when implementing banding:
- It is important to note that in the above log refers to the base 2 logarithm of a number.
- I found it useful to construct an array, bands, at the beginning of the COMPRESS operation, such that bands[Δ] is the band for the provided Δ.
- I used a very large constant to denote the band of Δ=0, as this made the tree-building operation simpler.
Compress
Compression in [GK01] is defined as follows:
- COMPRESS()
- for i from s–2 to 0 do …
However, with this definition, it is possible for the first (0th) tuple to be deleted, which would then violate the following invariant of the summary data structure: “We ensure that, at all times, the maximum and the minimum values are part of the summary.”
Therefore, I modified COMPRESS() to go from s–2 to 1 so that the first tuple is never deleted and the invariant is maintained.
References
- [GK01] M. Greenwald and S. Khanna. Space-efficient online computation of quantile summaries. In Proceedings of ACM SIGMOD, pages 58–66, 2001.